반응형
안녕하세요.
이번엔 제가 이해한 PCA 입니다. 제가 이해한 대로 작성하는 글이라 어디든 언제든 틀린 부분이 있을 수 있습니다
제 생각에 가장 기초가 되는 내용들입니다.
- 1변수 == 1차원
- 차원의 저주 : 수천 ~ 수백만개의 특성을 가졌을때 생기는 문제
- 차원의 저주 → 훈련 속도 저하 및 좋은 솔루션 탐색 방해
- MNIST → 거의 항상 흰색인 픽셀들은 제거해도 많은 정보를 잃지 않으며, 인접한 두 픽셀은 주로 연관되어 있는데, 이는 두 셀을 합쳐도 잃는 정보가 많지않음
[초평면 정의]
수학에서 초평면(超平面, 영어: hyperplane)은 3차원 공간 속의 평면을 일반화하여 얻는 개념이다.

8.1 차원의 저주
- 차원의 저주 : 3차원 이상부터는 상상하기 힘듦

- 고차원 데이터는 많은 공간을 가지고 있으므로 훈련 데이터가 매우 멀리 떨어져 있는데, 이는 새로운 샘플도 훈련 샘플과 멀리 떨어져 있을 가능성이 높음
- 저차원일때보다 예측이 불안정하며 과대적합의 위험이 커짐
- (이론상) 해결방법은 훈련 샘플의 밀도가 충분히 높아질 때까지 훈련 세트의 크기를 키우는 건데 사실상 불가능
8.2 차원 축소를 위한 접근 방법
- 투영 (projection), 매니폴드
8.2.1 투영
- 대부분의 실전 문제는 훈련 샘플이 모든 차원에 걸쳐 균일하게 퍼져 있지 않음
- 많은 특성은 거의 변화가 없으나 다른 특성들은 서로 강하게 연관되어 있음.
- 결과적으로 모든 훈련 샘플이 고차원 공간 안의 저차원 부분 공간(subspace)에 놓여있음 → 대부분이 특정 몇개의 변수에 대해 연관성을 가진다는 의미라고 이해함

- 모든 훈련 샘플이 거의 평면 형태인데 이게 3차원에 있는 2차원 부분공간임.
- x1,x2,x3이라 3차원으로 구성되어 있으나 데이터의 배치 자체는 2차원과 비슷한 형태를 가짐

- 회색 면과 샘플을 사이의 가장 짧은 거리를 따라서 수직으로 투영하면 2차원 데이터셋을 얻을 수 있음
- 새로운 특성인 z1,z2에 대응됨
- 그렇지만 투영이 늘 좋은 방법은 아님. 스위스 롤같은 형태의 데이터 셋도 존재

- x3을 제외하고 평면에 투영시키면

- 여기 왼쪽처럼 나오는데, 우리가 원하는건 오른쪽 처럼 예쁜모양임
8.2.2 매니폴드 학습
- 정의 : 내가 가진 학습 데이터셋에 존재하는 수많은 이미지를 고차원 공간 속에 매핑시키면 유사한 이미지는 특정 공간에 모여있을 것입니다. 그리고 그 점들의 집합을 잘 아우르는 전체 공간의 **부분집합(subspace)**이 존재할 수 있을텐데 그것을 우리는 매니폴드(manifold) 라고 함
- 스위스 롤은 2D 매니폴드의 하나의 예시임
- 2D 매니폴드는 고차원 공간에서 휘어지거나 뒤틀린 2D 모양
- 일반적으로 d차원 매니폴드는 국부적으로 d차원 초평면으로 보일 수 있는 n차원 공간의 일부 (d < n) : n차원에서 d차원 초 평면을 의미함
- 스위스롤의 경우 d=2, n=3
- 대부분의 차원 축소 알고리즘이 훈련 샘플이 놓여 있는 매니폴드를 모델링 하는 식으로 작동하며, 이를 매니폴드 학습이라고 함
- 실제 고차원 데이터셋이 더 낮은 저차원 매니폴드에 가깝게 놓여있다는 매니폴드 가정 또는 매니폴드 가설에 근거 (경험적으로 맞음)
- MNIST 예시 : 어느정도 자유도를 제한하여 중구난방의 이미지를 만들지 않아서 이런 제한된 자유도를 활용하여 데이터를 저차원의 매니폴드로 압축할 수 있음
- 매니폴드 가정은 종종 다른 가정과 병행됨
- 분류와 회귀같은 작업이 저차원의 매니폴드 공간에 표현되면 더 간단해질 것 이라는 가정
- 아래 예시를 보면 왼쪽 3차원 결정경계는 복잡하지만 오른쪽 2차원 결정경계는 훨씬 간단함

- 모델은 훈련시키기전 훈련 세트의 차원을 감소시키면 속도는 빨라지나 항상 더 좋은 솔루션이 되는 건 아님
8.3 PCA
- 가장 인기 있는 차원 축소 알고리즘으로 데이터에 가장 가까운 초평면을 정의한 후 데이터를 투영함
8.3.1 분산 보존
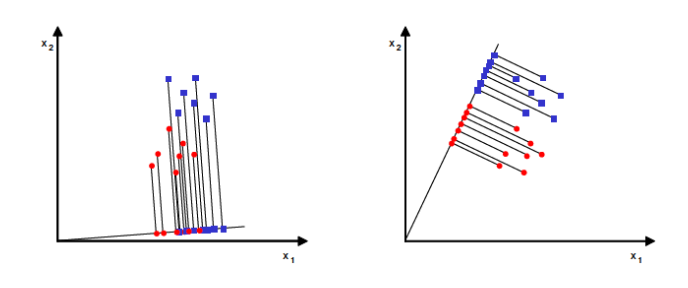
- 저차원의 초평면에 훈련 세트를 투영하기 전에 먼저 올바른 초평면을 선택해야함
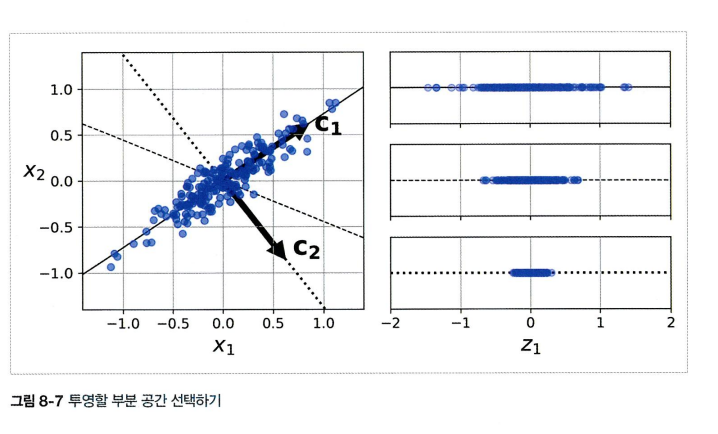
- 실선은 분산을 최대로 보존하는 반면 점선에 투영된 것은 분산을 매우 적게 유지하고 있음
- 다른 방향보다 분산이 최대로 보존되는 실선을 선택하는것이 정보가 가장 적게 손실되므로 합리적으로 보임 (= 원본 데이터셋과 투영된 것 사이의 평균 제곱 거리를 최소화 하는 축)
8.3.2 주성분
- PCA에서는 분산이 최대인 축(실선)을 찾고 이후 첫번째 축에 직교하고 남은 분산을 최대한 보존하는 두번째 축(점선)을 찾음
- 축 여러개 가능
- i번째 축을 i번째 주성분 PC(Principle Component)라고 부름
- 훈련세트의 주성분을 찾는 방법 : 특잇값 분해
8.3.3 d차원으로 투영하기
- 주성분을 추출했다면 처음 d개의 주성분으로 정의한 초평면에 투영하여 데이터셋의 차원을 d차원으로 축소 시킬 수 있음.

8.3.4~5 사이킷런 사용하기 ~ 설명된 분산의 비율 (colab)
8.3.6 적절한 차원 수 선택하기
- 차원의 수를 임의로 정하기 X
- 충분한 분산(ex 95%)이 될때까지 더해야 할 차원의 수 선택하기
- 데이터 시각화를 위해서 축소하는 경우는 2~3개의 차원으로 줄이는게 일반적
- elbow
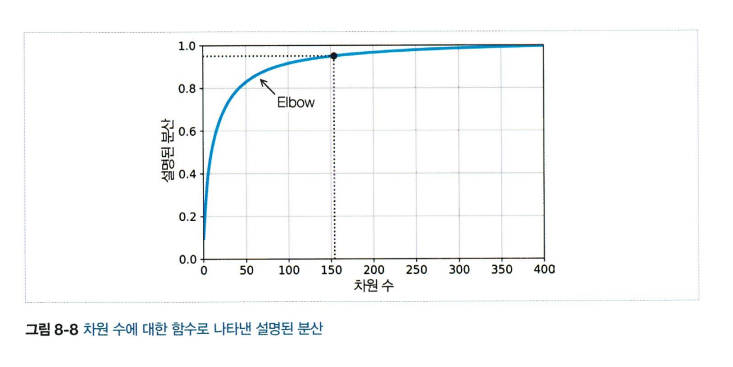
8.3.7 압축을 위한 PCA
- (분산 95%로) MNIST에 적용한 결과 784차원 → 150차원으로 축소 됨 (반대도 가능함)
- 분산은 유지하되 데이터셋은 원본 크기의 20% 미만이 되었음
- 원본 데이터와 재구성된 데이터 (압축후 원상복구한 것) 사이의 평균 제곱거리를 재구성 오차라고 함

8.3.8 랜덤 PCA
- 공분산 행렬의 고유 벡터를 계산할 필요 없이 큰 데이터 집합의 주성분 근사치를 구하는 방법
- 데이터에 랜덤화 선형 변환을 적용함으로써 작동하며, 이는 적은 수의 샘플을 사용하여 주요 주성분의 근사치를 얻을 수 있게 함
- PCA보다 빠르며 매우 큰 데이터 집합으로 작업할 때 유용함
8.3.9 점진적 PCA (IPCA)
- 훈련세트를 미니배치로 나눈 뒤 IPCA 알고리즘에 한번에 하나씩 주입함
- 훈련세트가 클 때도 유용하고 온라인 (새로운 데이터가 준비되는 대로 실시간으로) PCA를 적용 할 수 있음
8.4 커널 PCA
- 비선형 함수인 커널함수를 이용하여 비선형 데이터를 고차원 공간으로 매핑하는 기술
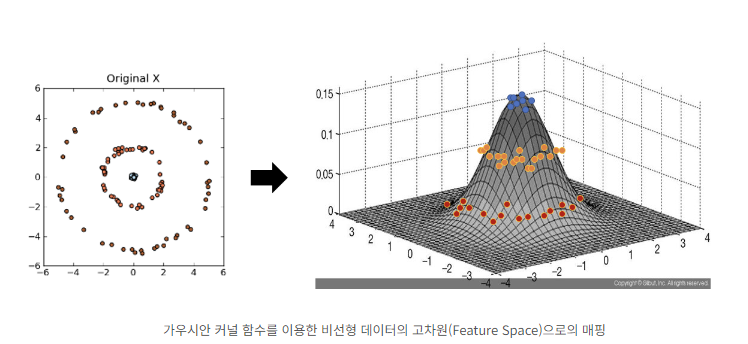
- 선형 변환으로 데이터를 분류하기 어려운 경우 커널 함수를 사용하여 데이터 분포를 분류할 수 있는 결정경계를 찾음
- 투영된 후 샘플의 군집을 유지하거나 꼬인 매니폴드에 가까운 데이터셋을 펼칠 때도 유용함
- 선형, RBF, 시그모이드 커널을 사용하여 2차원으로 축소시킨 스위스 롤
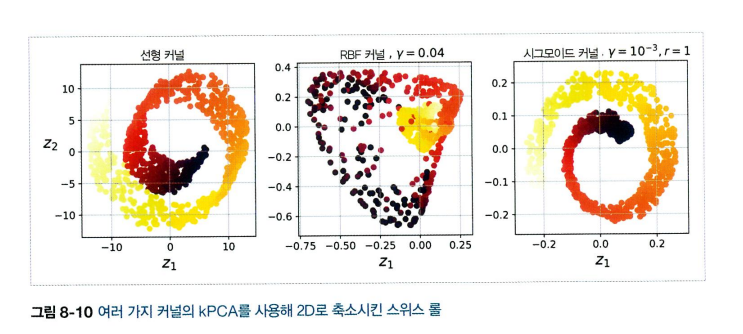
8.4.1 커널 선택과 하이퍼파라미터 튜닝
- KPCA는 비지도 학습이므로 명확한 성능 측정의 기준이 없으나 종종 지도 학습의 전처리 단계로 활용되므로 그리드 탐색을 사용하여 주어진 문제에서 성능이 가장 좋은 커널과 하이퍼 파라미터를 선택할 수 있음
- 차원축소 → 로지스틱회귀 → 그리드서치를 활용하여 커널과 하이퍼파라미터 찾기

- 왼쪽 위 : 원본 3D 데이터 셋
- 오른쪽 위 : RBF 커널의 KPCA를 적용한 2D 데이터셋
- 오른쪽 아래 : 특성맵을 활용하여 훈련 세트를 무한 차원의 특성 공간에 매핑한 것
- 왼쪽 아래 : 재구성된 원상 ← ?? 여기부터 이해 못했습니다
8.5 LLE (지역 선형 임베딩)
- 비선형 차원 축소 기술
- 각 훈련 샘플이 가장 가까운 이웃에 얼마나 선형적으로 연관되어 있는지 측정한 후, 국부적인 관계가 가장 잘 보존되는 훈련 세트의 저차원 표현을 찾는다.

- 데이터 포인트 Xi에 대해 가장 가까운 k 개의 이웃을 구한다 (knn)
- 현재 데이터를 나머지 k개의 데이터의 가중치 합을 뺄 때 최소가 되는 가중치 매트릭스를 구한다
- 앞서 구한 가중치를 최대한 보장하며 차원을 축소함. 이때 차원 축소된 점은 Y로 표현하며, Yi와의 값 차이를 최소화하는 Y를 찾음
8.6 다른 차원 축소 기법
(참고 : https://woosikyang.github.io/first-post.html)
- 랜덤 투영 : 랜덤 선형 투영을 사용하여 데이터를 저차원 공간으로 투영함 (실제거리를 잘 보존하는것으로 증명됨)
- 다차원 스케일링 (MDS) : 샘플간의 거리를 보존하며 차원 축소
- lsomap : 각 샘플을 가장 가까운 이웃과 연결하는 식으로 그래프를 만듦

- t-SNE : 비슷한 샘플은 가까이, 비슷하지 않은 샘플은 멀리 떨어지도록 하며 차원 축소 (시각화 | 군집 시각화 등에 주로 사용됨)
- LDA (선형 판별 분석)
반응형
'머신러닝' 카테고리의 다른 글
| [결정트리] 내가 이해한 결정트리 (0) | 2024.05.21 |
|---|---|
| [배깅,부스팅] 내가 이해한 배깅 및 부스팅 방법론 (1) | 2024.05.21 |
| [정규화] 내가 이해한 릿지, 라쏘, 일라스틱넷 (0) | 2024.05.15 |



댓글