[정규화] 내가 이해한 릿지, 라쏘, 일라스틱넷

안녕하세요. 

의료 AI에 관심이 있어, 현재 석사 과정중인데, 머신러닝 자체 스터디 중 공부한 내용이 혹시나 도움이 될까 공유합니다. 

제가 이해한 대로 적은 글이라 얼마든지 틀릴 가능성이 존재합니다,, 

 

릿지, 라쏘, 일라스틱넷은 정규화 방식으로 MSE를 어느정도 올리면서, 모델의 과적합을 방지하는 방법입니다. 

본 글은 가장 많이 도움을 받았고, 가장 쉽게 이해할 수 있었던 유튜브 "김성범[교수 / 산업경영공학부]" 채널을 기반으로 작성되었습니다. (https://www.youtube.com/watch?v=sGTWFCq5OKM) 1,2편으로 구성되어있는데 정말 알차고 쉽습니다.

 

 

위 그림과 같이 과대적합된 모델에 정규화를 적용하여 과대적합을 줄이기 위한 과정으로 릿지, 라쏘, 일라스틱넷의 방법이 있음

 

- 정규화 기본 컨셉

그림에서 알 수 있듯 빨간색 데이터에 대해서 초록색으로 그래프를 그렸는데 각각 1차, 2차, 4차의 그래프이다. 1차 그래프의 경우 과소적합의 문제가 있으며, 4차 그래프의 경우 과대적합의 문제가 있다.

아래에 있는 그래프는 X축이 차원, Y축이 에러이다. 차원이 너무 낮으면 훈련과 테스트 데이터셋에서 높은 편향을 보이고 차원이 너무 높아지면 과대적합으로 인해 훈련 데이터에서는 에러가 낮으나 테스트 데이터셋에 대해서는 에러가 커진다.

따라서 우리는 4차 그래프를 2차로 변형해야 하는데 이때 쓰이는게 정규화이다

정규화는 규제를 가하는것을 의미하는데 말로 듣는거보다는 그림을 보는게 이해가 쉽다.

위에 표에서 각 b1,b2의 값과 제곱합값, 그리고 MSE를 나타내고 있다 이때 우리는 MSE가 20으로 가장 낮은 B1,B2인 4,5를 사용하면 되지만 만약 이때 B12 + B22 이 30보다 작거나 같아야 한다는 규제를 걸어본다고 하자. 그러면 우리는 이 중에서 가장 MSE가 작은 B1,B2 값을 선택하게 될거다.

 

1. 릿지

 

여기서 MSE Contour를 간단하게 보고 가자

여기서는 b1,b2에 대한 mse를 간단하게 전개하는데 이때 맨 아래의 값이 Conic equation이 된다.

 

위에서 도출된 값을 판별식을 사용하여 해를 구하는데 이때 코시 슈바르츠 부등식을 사용하여 구한다. 따라서 결과적으로 타원이라는 결과가 나오게 된다.

 

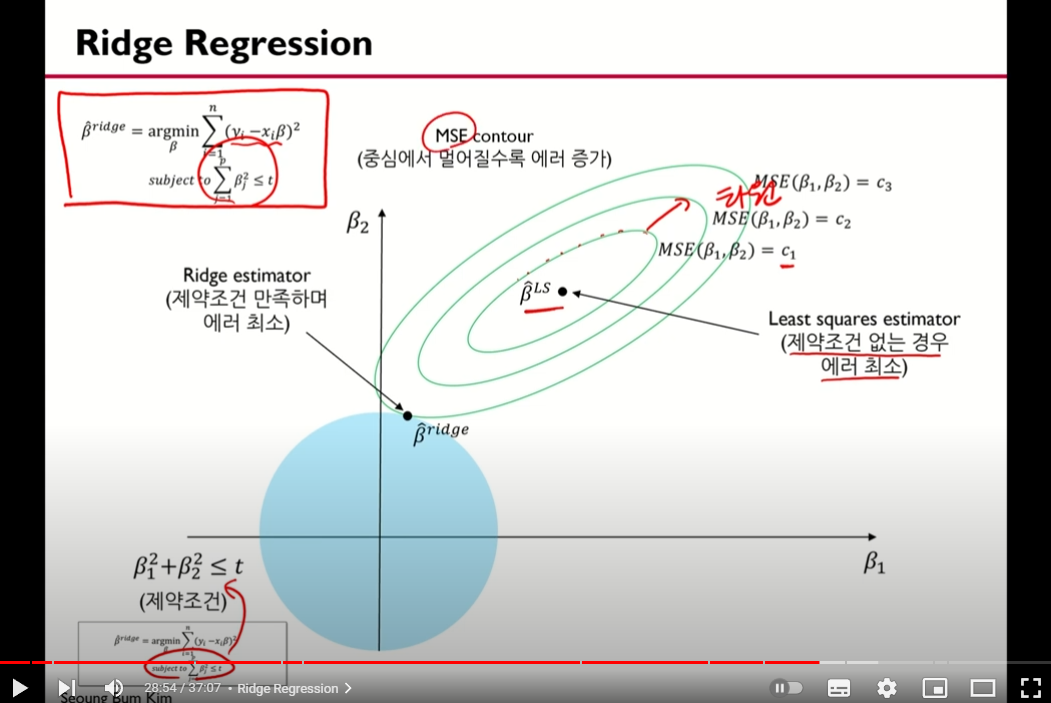
위의 과정을 거친건 타원 그림의 이해를 돕기 위함이다. 우리가 봤던 표에서 나와있는 값들은 최소제곱법을 활용하여 구한 b1,b2값들인데 이 값들의 집합이 타원으로 나타나있다 (추측임)

위에서 말했든 릿지회귀는 b1,b2값의 제곱 합에 대한 규제를 정했기 때문에 원모양으로 나타난다 (원의방정식) 따라서 그림의 파란원은 규제영역이다.

초록색 타원은 위에서 살펴본 MSE Contour의 결론이 타원으로 나왔으므로 타원을 점점 키워가면서 규제영역과 맞닿는 점을 찾는데 이게 릿지 회귀를 통해 찾은 b1,b2값이다.

맞닿는 점을 찾는 이유는 타원이 커지는건 곧 MSE가 커지는것을 의미하기 때문에 정규화를 하면서 mse를 최소한으로 늘리는 점이기 때문임

 

2. 라쏘

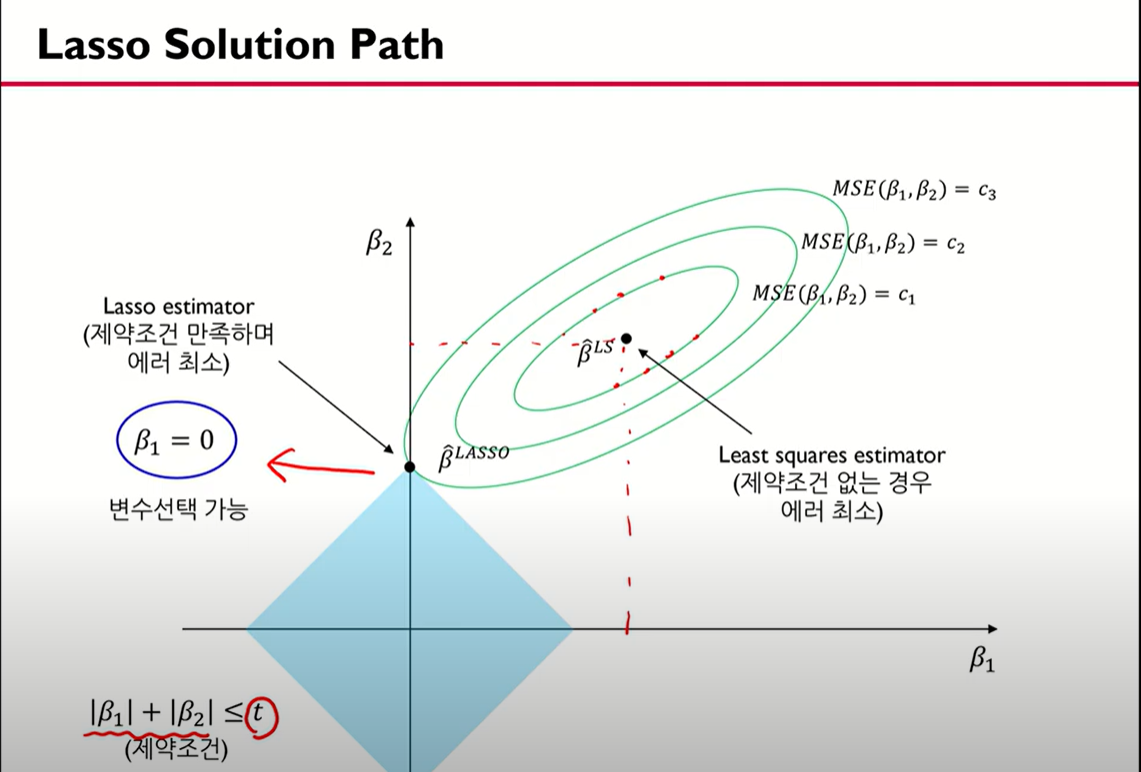
릿지와 비슷한데 릿지는 제곱을 사용하지만 라쏘는 절대값을 사용한다. 그래서 릿지는 원 모양이었으나 라쏘는 사각형 모양이 된다. 또 라쏘가 릿지와 다른 점은 변수 선택이 가능하다는 점이다. 여기서 말하는 변수 선택은 y값을 예측할 때 중요한 X를 선택 하는 것을 의미한다.

여기서 보면 중간에 b1=0으로 나타나있는데, 확장한 MSE Contour가 규제 영역과 만나는 부분이 B1=0가 되는 부분이기 때문이다. 그래서 라쏘는 변수 선택 기능까지 제공한다 (b1=0이라는 건 사실상 쓸모 없는 변수라는 의미가 되기 때문)

또한 라쏘는 릿지와 다르게 사각형이다. 사각형은 꼭짓점을 가지고 있어서 해당 부분은 미분이 불가능하다는 특징이 있어 closed form solution을 구하는 것이 불가능하여 Numerical Optimization Method를 사용한다. (자세히 안다룸)

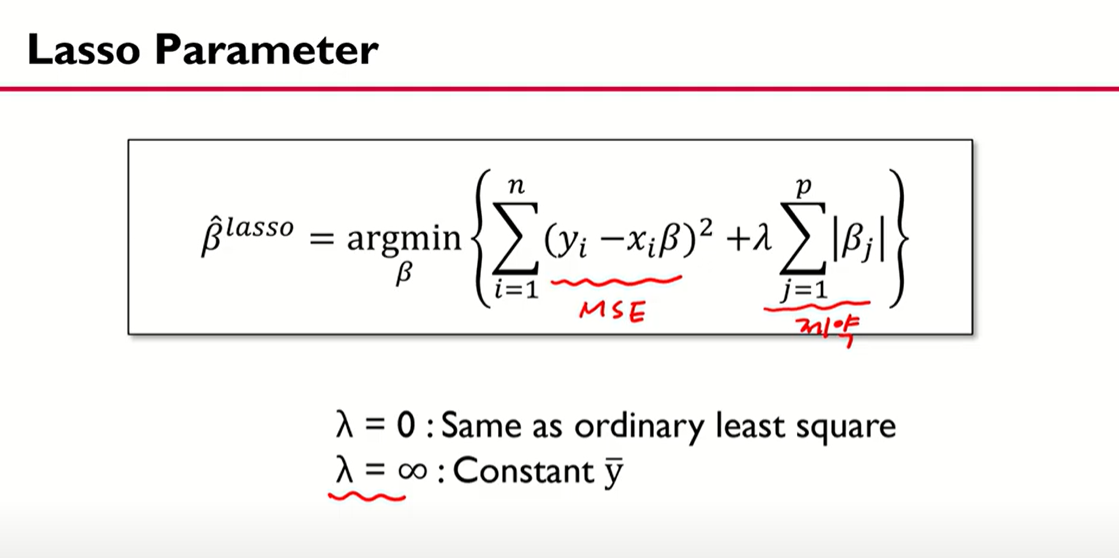
라쏘 함수 식인데 뒤에 람다가 제약조건 T와 같은 역할을 한다.

제약조건 T가 줄어들면, 제약이 커지고, 람다도 커진다. 반대로 제약조건 T가 늘어나면 제약이 작아지고 람다도 작아진다.

따라서 여기서 람다가 0이 되면 사실상 최소제곱법과 비슷하게 되고 람다가 너무 커지게 되면 균등분포와 비슷한 모양을 띄게 된다 (사실 이해 못함)

좀 더 자세한 설명을 같이 보자

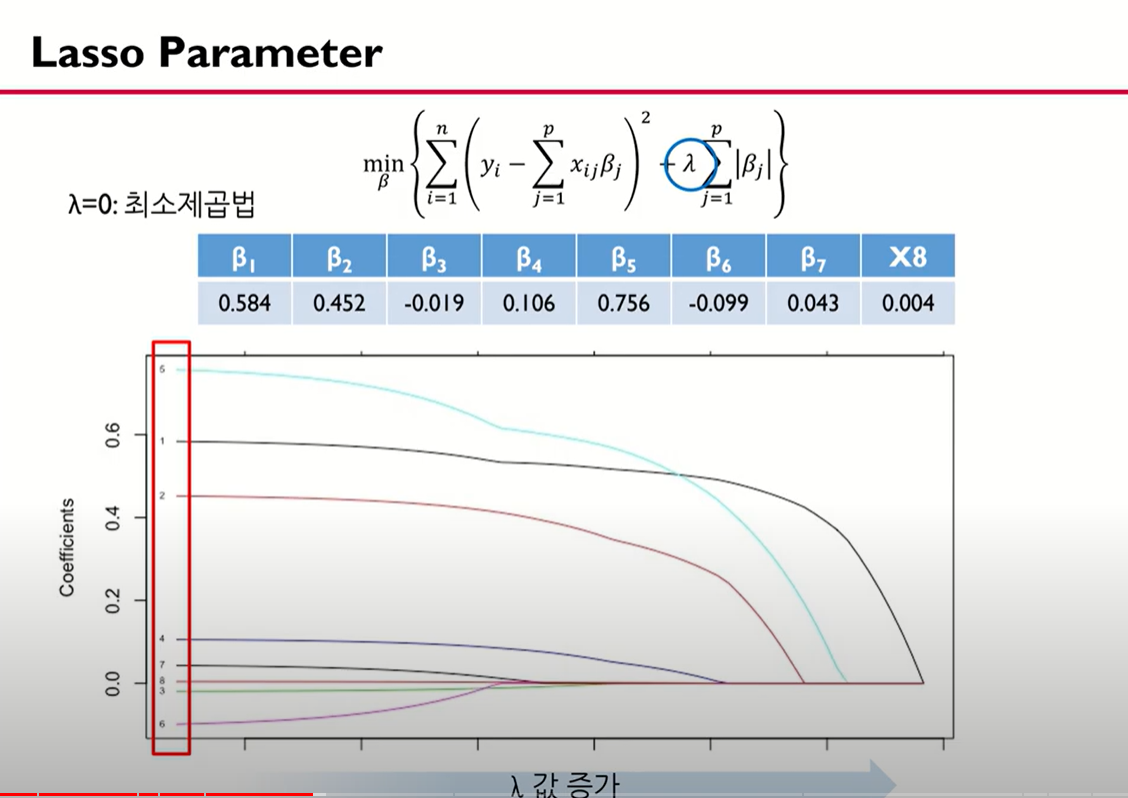
람다가 점점 커질수록 0에 수렴하는 변수들이 많아지는데 이는 람다가 커질수록 필요 없는 변수들이 많아지는것을 의미함 그렇기 때문에 라쏘는 데이터가 달라질 때마다 변수 선택이 달라질 수 있는 가능성이 있다.

릿지와 라쏘 비교이다

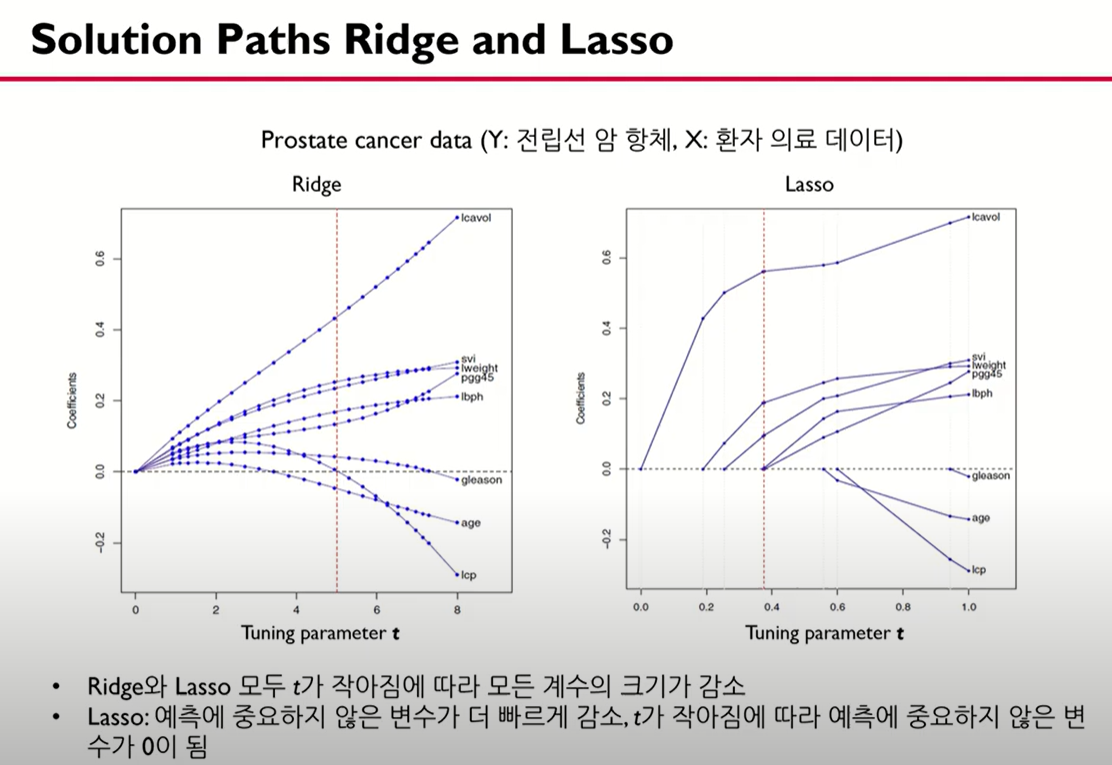
보면 릿지와 라쏘 모두 제약 조건이 작아짐(람다가 커짐)에 따라서 모든 계수의 크기가 감소하기는 하나 릿지는 0에 수렴하지 않지만 라쏘는 0에 수렴하는 모습을 보여서 변수 선택 기능을 가지고 있음을 알 수 있음

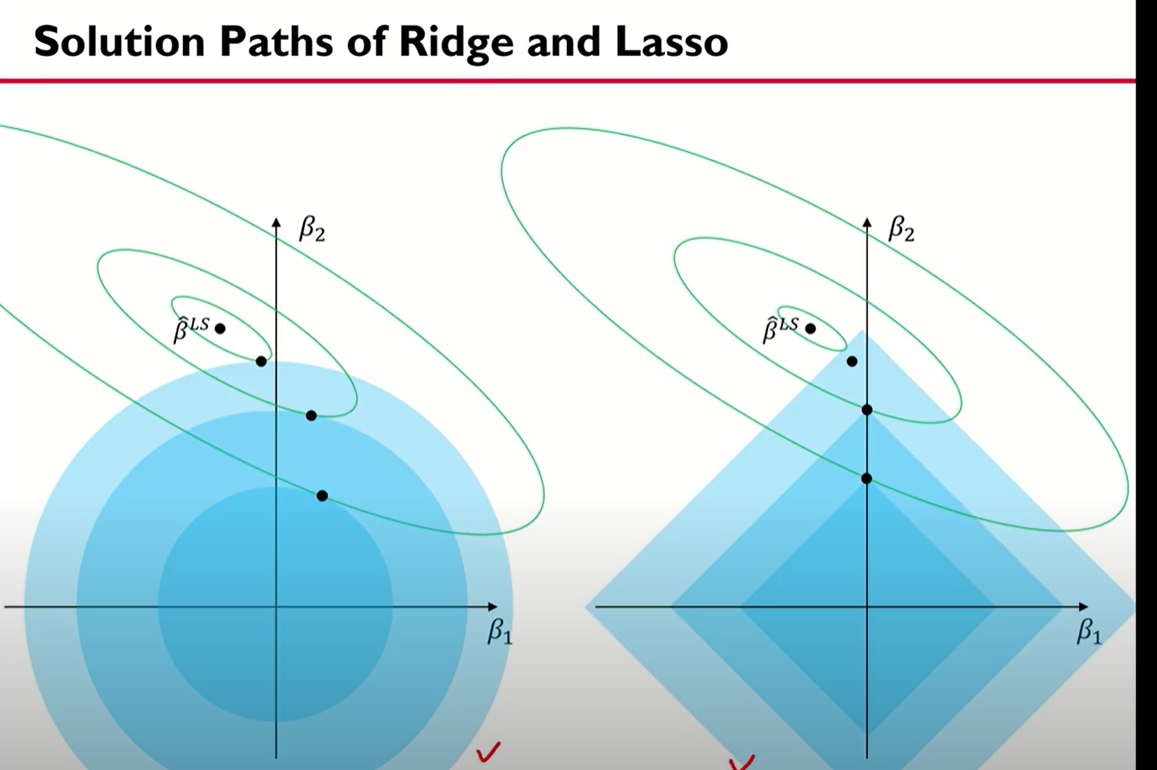
또 다른 그래프를 보면 왼쪽이 릿지 오른쪽이 라쏘인데, 릿지에서는 b1=0이 되는 점이 없으나 라쏘에서는 b1=0이 되는 부분이 존재함

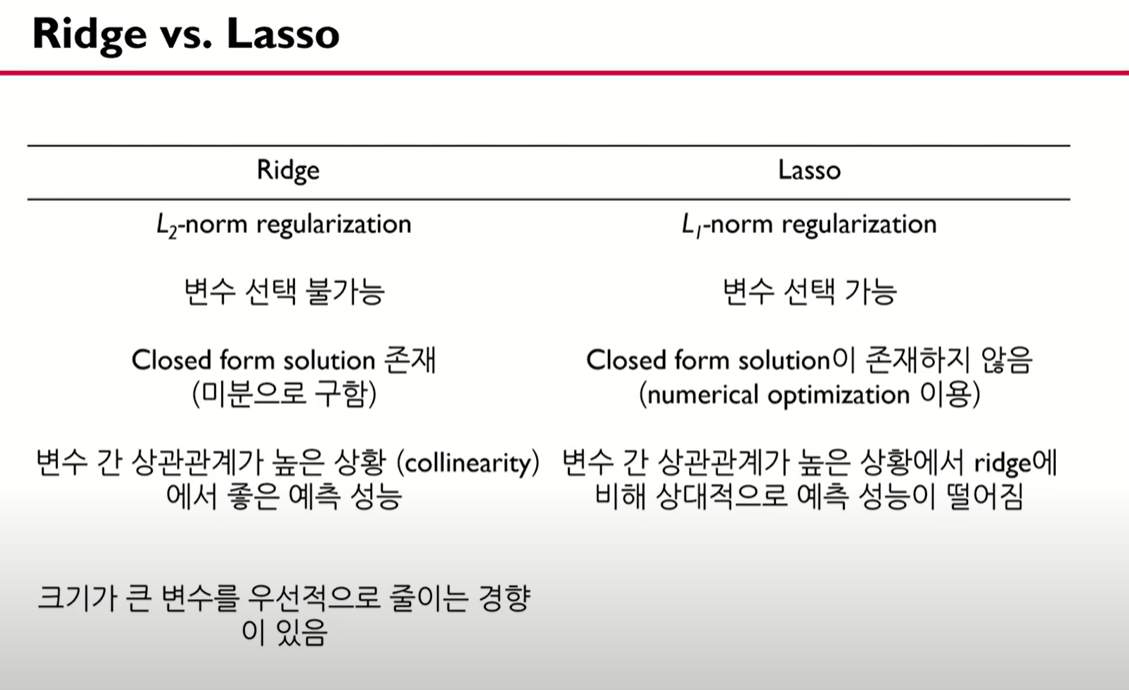
릿지와 라쏘의 차이점으로 변수 선택에 차이가 있고, 미분 여부에 따라서 colsed form solution 이 가능한지도 차이가 난다.

변수 간 상관관계가 높은 상황에서 릿지에 비해 상대적으로 예측 성능이 떨어짐 :

변수들의 상관관계가 큰 경우 변수 선택 성능이 저하되며 예측 성능도 저하됨 또한 변수 간 상관관계를 반영 할 수 있는 방법이 필요함

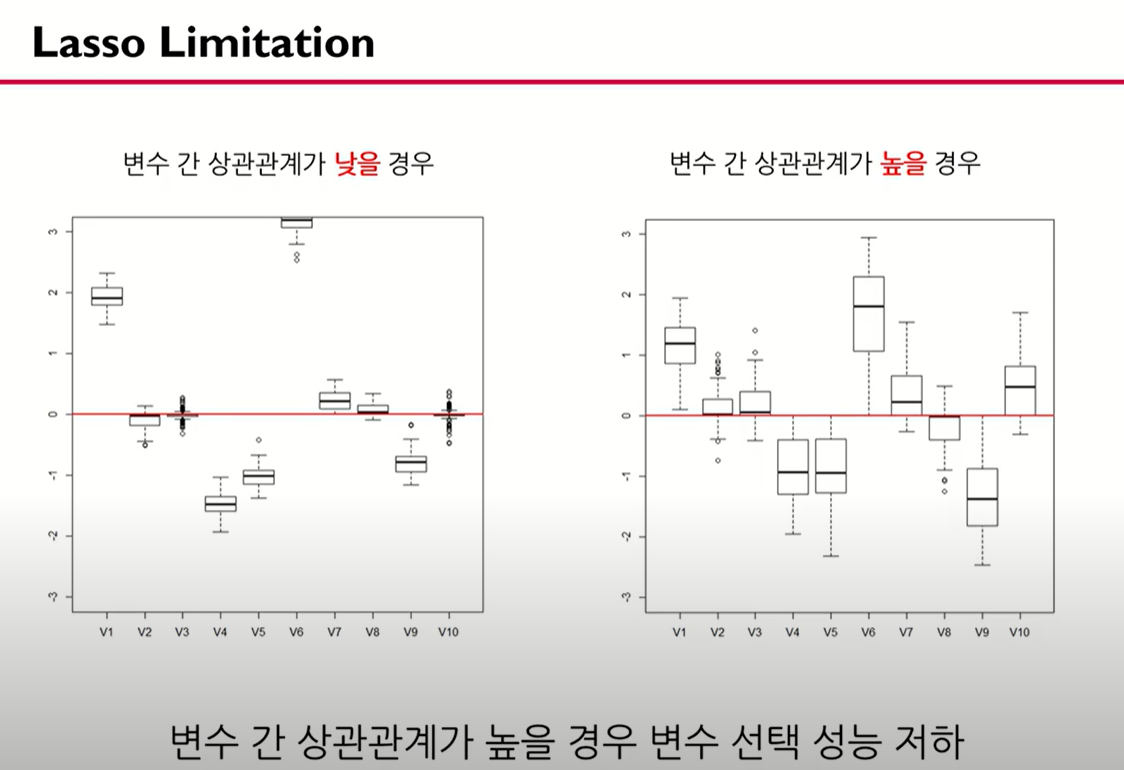
상관 관계가 낮은 경우 : 데이터가 변화함에 따라서 베타값이 크게 변화하지 않음 모델이 로버스트

상관 관계가 높은 경우 : 데이터가 변화함에 따라서 박스가 커짐.

 

3. 일라스틱넷

이 문제를 해결하기 위해 나온게 일라스틱 넷임

일라스틱 넷 : 릿지 + 라쏘의 제약을 동시에 함

제약식이 두개

보면 bi - bj를 하게 되면 아래와 같은 결과를 얻게 되는데 이때 p(로)는 상관계수를 의미함 상관계수가 1인 경우 윗 식에 대입시키면 bi = bj 으로 추정 할 수 있음 = 중요하면 똑같이 중요하다

변수와 그 변수와 상관 관계가 있는 변수는 같은 패턴으로 추정하겠다는 뜻임 = grouping effect

람다1 람다2는 그리드 서치를 통해서 조절함

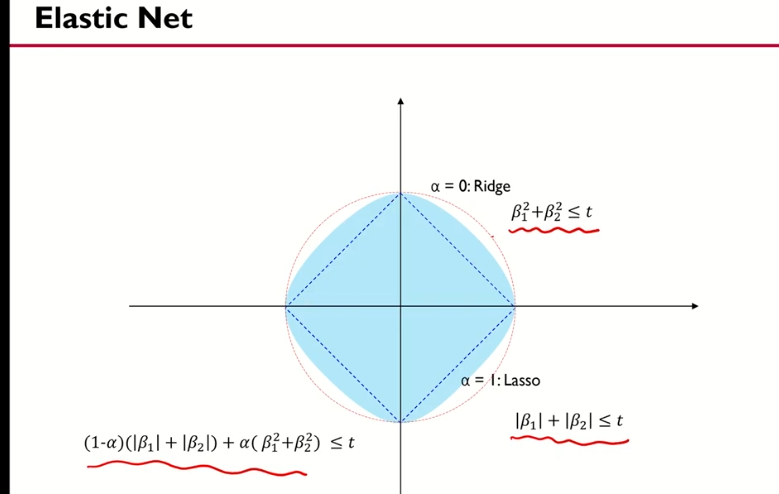
일라스틱넷 : 원도 마름모도 아님 릿지와 라쏘 사이의 느낌

 

 

 

+) 외에 개인적으로 궁금했던 부분을 추가합니다

위 내용을 기반으로 하면 릿지에서는 feature selection이 불가능한것으로 알고있는데, 한 논문에서 릿지를 활용하여 feature selection을 하였다고 해서 관련 내용을 찾아봤습니다. 

 

https://seongyun-dev.tistory.com/52 를 참고하면 릿지와 라쏘는 과적합을 방지하기 위해서 가중치는 주는 방법인데 라쏘는 가중치로 0을 주는것이 가능해서 변수 선택이 가능함 그렇지만 릿지는 0과 비슷한 수들 0.01,0.02등… 까지 가중치로 주는것이 가능해서 임계값을 0.01,0.02로 줘서 그 이상인지 이하인지로 변수 선택이 가능함.